Xusheng Chen's Homepage | About ballots in Paxos

Recently I am reading papers about asynchronous consensus protocols, and I was trying to contrast these protocols with Paxos (Lamport, 2001) and PBFT (Castro et al., 1999). When re-reading the Paxos paper, some of the design points take me some time to reason about. These thoughts may seem naive for Paxos experts, but I will just jot them down.

In Paxos, a value is confirmed only if it is accepted with the same ballot by a majority of acceptors. Why is having a majority of acceptors accept the same value not enough?

(At first, I thought the accept action in Paxos corresponds to decide in Ben-Or’s algorithm (Ben-Or, 1983), and thus I was wondering why Ben-Or’s algorithm can let nodes decide a value in different rounds, but Paxos requires a majority of nodes to accept with the same ballot. However, this comparison is wrong. Ben-Or’s decide is more like the behavior of learners in Paxos, and Ben-Or’s algorithm can be regarded as skipping the first phase of Paxos if we have to parallelize them.)

To answer this question, we can simply construct a counterexample which shows that, after a majority of acceptors have accepted a same value $v$ with different ballots, the system may decide a different value $v^{'}$ . I will use $(n, v)$ to denote a proposal of value $v$ with ballot $n$ .

Let’s use the simplest setting with 3 acceptors $A_{1}, A_{2}, A_{3}$ , where $A_{1}$ has accepted $(n_{1}, v)$ and $A_{2}$ has accepted $(n_{2}, v)$ . Without losing generality, let $n_{1} < n_{2}$ . Now we want one of them to switch to accept another value $(n^{'}, v^{'})$ (after which another proposer can let the system accept $v^{'}$ by forming a majority with $A_{3}$ ). For simplicity, we assume there are no other concurrent proposals.

If the prepare message of $n’$ arrives after $A_{1}$ and $A_{2}$ accept $v$ , its proposer will learn and propose $v$ , so at least one of $A_{1}$ and $A_{2}$ must prepare $n^{'}$ before accepting $v$ . On the other hand, $n^{'}$ cannot be smaller than both $n_{1}$ and $n_{2}$ , otherwise they will ignore the accept message for $v^{'}$ , so we have $n_{1} < n^{'} < n_{2}$ .

We visualize the construction below. A new proposer can use $A_{1}, A_{3}$ to form a majority, and let the system accept $v_{2}$ at the end, even if two acceptors have accepted $v_{1}$ with different ballots at some time.

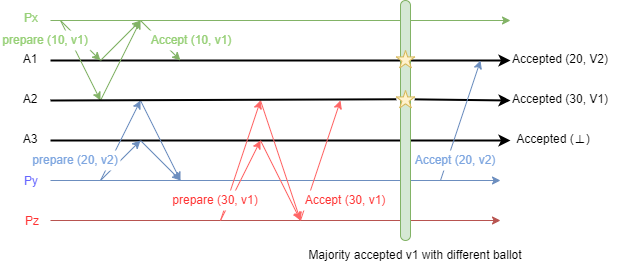
Paxos-Ballot

Overall, in Paxos, although an acceptor will try to let subsequent proposers follow its accepted value, the proposer can find a majority/quorum without including this acceptor. Even if a majority of acceptors accept the same value $v$ , if they are not of the same ballot, another proposer can still succeed in letting a majority of acceptors prepare a ballot that lies in the gap among the accepted ballots for $v$ before they all accept $v$ .

This makes me think about another possible design. What if we can have a method that makes there no gap between the ballots for accepting the same value? I did not conduct a formal proof, but it seems to be enough for correctness. However, how can we ensure there are no new ballots can be inserted? Using consecutive integers? Using
timestamps and safe timestamp mechanism?

Another thought is about the proposed value. In Ben-Or’s algorithm, a node tries to follow the value from other nodes in its Phase-1 in order to facilitate convergence. In contrast, in Phase-1 of Paxos, the proposer does not follow the value prepared by acceptors; its proposed value is affected only by accepted values.

What if we adapt Paxos and let a proposer follow the value observed in Phase-1. I was thinking this may make it possible to enable Paxos to confirm a value by accepting it value with different ballots. However, by simple variants of the previous construction, we can see that it is not correct. However, will this adaption cannot make the consecutive-ballot design viable?

Anyway, these are just some random thought, and I did not spend much time to verify them, as the vanilla Paxos (Paxos-made-simple without a stable leader) is rarely used in deployments.

References:

Leslie Lamport . Paxos made simple. ACM SIGACT News (Distributed Computing Column) 32, 4 (Whole Number 121, December 2001) 2001
Miguel Castro, Barbara Liskov, and others . Practical byzantine fault tolerance. In OsDI 1999
Michael Ben-Or . Another advantage of free choice (extended abstract) completely asynchronous agreement protocols. In Proceedings of the second annual ACM symposium on Principles of distributed computing 1983